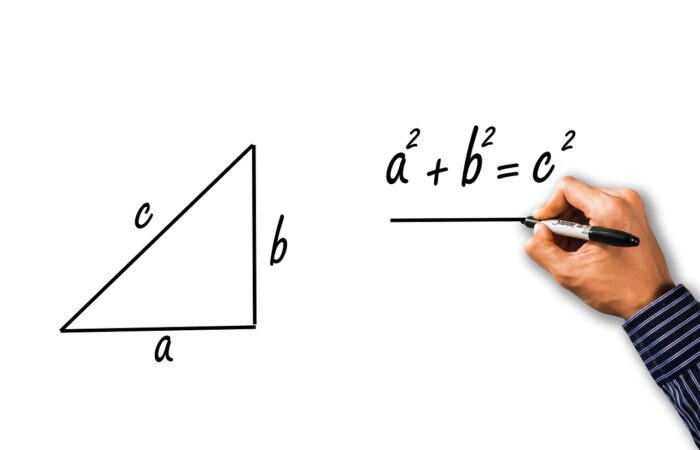Brève introduction à la géométrie
La géométrie, héritière des observations et des calculs des anciennes civilisations, tient une place fondamentale en mathématiques. Son domaine d’étude porte sur les dimensions, les formes, les figures et les espaces. Depuis ses origines, elle n’a cessé d’évoluer et d’intégrer de nouveaux concepts. Mais parmi tous ceux-ci, certains ont traversé les siècles sans prendre une ride. Le Théorème de Pythagore en est sans doute le meilleur exemple.
Présentation du thème : le Théorème de Pythagore
Le Théorème de Pythagore est probablement l’un des énoncés mathématiques les plus connus. Il doit son nom à Pythagore, même si ses origines remontent à bien avant l’Antiquité grecque. Il s’agit d’une formule simple, mais profonde, qui lie les longueurs des côtés d’un triangle rectangle. Plus précisément, il indique que le carré de la longueur de l’hypoténuse équivau à la somme des carrés des longueurs des deux autres côtés. C’est une règle fondamentale de la géométrie euclidienne.
Comprendre le Théorème de Pythagore
Présentation et explication du Théorème de Pythagore
Le Théorème de Pythagore est une proposition géométrique fondamentale qui tient en une seule phrase : dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés. Cette affirmation peut se traduire par la formule c² = a² + b², où c représente la longueur de l’hypoténuse, et a et b celles des deux autres côtés.
Importance du Théorème de Pythagore dans différents domaines
Le Théorème de Pythagore est bien plus qu’un simple outil pour résoudre des problèmes de géométrie. Ses implications s’étendent à de nombreux autres domaines, de la physique à l’ingénierie en passant par l’architecture et même l’astronomie. En maîtrisant le Théorème de Pythagore, vous devenez non seulement plus à l’aise avec les problèmes mathématiques, mais vous acquérez aussi une meilleure compréhension de l’espace et de la distance dans le monde qui vous entoure.
Illustration du Théorème de Pythagore à l’aide d’exemples concrets
Supposons que vous ayez un triangle rectangle avec les côtés ‘a’ et ‘b’ mesurant respectivement 3 et 4 unités. En appliquant le Théorème de Pythagore, vous pouvez calculer l’hypoténuse ‘c’ en résolvant c² = a² + b².
Donc, c² = 3² + 4², qui équivaut à c² = 9 + 16. En simplifiant, on obtient c² = 25.
Pour trouver la longueur de ‘c’, il suffit maintenant de prendre la racine carrée des deux côtés de cette dernière équation. On obtient donc c = √25, ce qui donne c = 5 unités. C’est aussi simple que cela.
Comment déterminer l’hypoténuse d’un triangle rectangle ?
Explication des termes : hypoténuse, côté adjacent, côté opposé
- 1. Hypoténuse : l’hypoténuse est le côté le plus long d’un triangle rectangle. Elle est opposée à l’angle droit du triangle. Son nom vient du grec hypotenusa, qui signifie « qui est étendu sous ». En d’autres termes, pour un observateur situé à l’un des angles aigus du triangle, l’hypoténuse se présente comme la base sur laquelle repose le triangle rectangle.
- 2. Côté adjacent : le côté adjacent est celui qui touche à la fois l’angle droit et l’angle d’intérêt. Sa longueur est généralement désignée par le symbole ‘a’.
- 3. Côté opposé : le côté opposé est celui qui est le plus éloigné de l’angle d’intérêt. Sa longueur est généralement désignée par le symbole ‘b’.
Etapes pour calculer l’hypoténuse d’un triangle rectangle
- 1. Appliquez le Théorème de Pythagore : c² = a² + b². Cette formule exprime le fait que le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés.
- 2. Insérez dans cette formule les valeurs connues de ‘a’ et ‘b’. Ces valeurs doivent être exprimées dans la même unité de mesure (mètres, centimètres, etc.).
- 3. Calculez ensuite la somme des carrés de ‘a’ et ‘b’. C’est-à-dire, calculez a² + b².
- 4. Pour trouver la valeur de ‘c’, prenez la racine carrée de cette somme. La racine carrée d’un nombre x est le nombre qui, multiplié par lui-même, donne x. En d’autres termes, c’est l’opération inverse du carré.
Illustration à travers des exemples pratiques
Essayons maintenant de mettre ces instructions en pratique. Prenons l’exemple d’un triangle rectangle dont ‘a’ mesure 6 unités et ‘b’ 8 unités. La formule c² = a² + b² devient alors c² = 6² + 8².
En effectuant les opérations nécessaires, on obtient c² = 36 + 64, soit c² = 100.
Pour trouver la longueur de l’hypoténuse, il suffit de prendre la racine carrée des deux côtés de cette équation, ce qui donne c = √100. Ainsi, la longueur de l’hypoténuse est de 10 unités.
Exercices pratiques
Proposer des problèmes simples de calcul de l’hypoténuse
Pour mettre en pratique ce que vous avez appris jusqu’ici, essayez de résoudre les problèmes suivants en utilisant le Théorème de Pythagore :
- 1. Pour un triangle rectangle avec ‘a’ = 5 unités et ‘b’ = 12 unités, quelle est la longueur de l’hypoténuse ? Vous pouvez utiliser la formule c = √(a² + b²) pour résoudre ce problème.
- 2. Si ‘a’ = 7 unités et l’hypoténuse, ‘c’ = 25 unités, quelle est la longueur du côté ‘b’ ? Dans ce cas, nous savons déjà la valeur de l’hypoténuse. Nous devons donc réarranger la formule du théorème de Pythagore pour trouver la valeur de ‘b’. La formule devient alors b = √(c² – a²).
Solutions détaillées avec explications pour chaque problème
Voici comment résoudre les problèmes ci-dessus :
- 1. Pour trouver l’hypoténuse, on applique la formule c = √(a² + b²), qui devient c = √(5² + 12²). On obtient donc c = √(25 + 144) = √169, soit c = 13 unités.
- 2. Pour trouver la longueur de ‘b’, on utilise la formule b = √(c² – a²), qui devient b = √(25² – 7²). On obtient donc b = √(625 – 49) = √576, soit b = 24 unités.
Conclusion
Que vous soyez étudiant en mathématiques, architecte, ingénieur, astronome ou simplement une personne qui souhaite mieux comprendre le monde qui l’entoure, l’utilisation du Théorème de Pythagore vous sera certainement utile à un moment donné. Ce théorème vous permet de maîtriser un des aspects fondamentaux de la géométrie, mais aussi de comprendre les lois fondamentales qui gouvernent l’espace et la distance.
Le Théorème de Pythagore a de nombreuses autres applications en dehors du domaine de la géométrie. Il est utilisé par exemple dans les systèmes de navigation GPS pour déterminer les distances, dans la conception d’infrastructures routières pour déterminer le trajet le plus court, dans celle d’appareils électroniques pour optimiser l’emplacement des composants, et même dans des domaines artistiques pour créer des effets de perspective. Que vous soyez dans un musée d’art ou en randonnée avec un GPS, vous pouvez être sûr que le Théorème de Pythagore n’est pas loin !